임의의 집합 data의 모든 부분집합을 출력하라
data = {a,b,c,d}
공집합
a
b
c
d
a b
a c
a d
b c . . .
2의 4(원소갯수)승 = 16개
{a,b,c,d,e,f}의 모든 부분집합을 나열하려면
a를 제외한 {b,c,d,e,f}의 모든 부분집합들을 나열하고
{b,c,d,e,f}의 모든 부분집합에 {a}를 추가한 집합들을 나열한다.
powerSet(S)
if s is an empty set
print nothing;
else
let t be the first element of s;
find all subsets of s-[t] by calling powerSet(s-{t});
print the subsets;
print thet subsets with adding t;Pseudo code
입력으로 하나의 집합 s가 주어진다.
s의 멱집합을 출력하는 것이 미션이다.
base case
만약 s가 공집합이라면 공집합을 출력한다.
그렇지 않다면
집합s에서 한 원소t에 대해서 t를 제외한 집합의 부분집합을 구한다.
그 부분집합을 출력하고
제외했던 원소를 추가하여 출력한다
s-{t}의 부분집합을 구한 후 그 부분집합을 한번은 그대로 출력하고 한번은 t를 추가해 출력하려면
powerSet함수는 여러개의 집합들을 return 해야한다. 어떻게 해야할까
powerSet(P,S)
if S is an empty set
print p;
else
let t be the first element of S;
powerSet(P, S-{t});
powerSet(Pu{t}, S-{t});처음 호출할때 P를 공집합 S가 전체데이터 집합 이라면
S의 멱집합을 구한 후 각각에 집합 P를 합집합하여 출력하도록 설계해야한다.
base case
만약 s가 공집합이라면 집합 P 출력
그렇지 않다면 t에 대해서 s에서 t를 제외하여 호출하고
t를 포함하여 P에 합쳐두어 출력하게 만든다.
함수가 두 개의 집합을 매개변수로 받도록 설계해야한다는 의미이다.
두 개의 집합의 모든 부분집합들에 첫접째 집합을 합집합 하여 출력한다.
두 개의 집합으로 나뉘게되면
집합 S : k번째 부터 마지막 원소까지 연속된 원소들이다.
집합 P : 처음부터 k-1째 원소들 중 일부이다.
boolean배열을 사용하여
집합 P를 구현할 수 있다.
private static char data[] = {'a','b''c','d','e','f'};
private static int n = data.length;
private static boolean [] include = new boolean[n];
public static void powerSet(int k) {
if(k==n){
for(int i =0; i<n; i++)
if(include[i]) System.out.print(data[i] + " ");
System.out.println();
retrun;
}
include[k] = false;
powerSet(k+1);
include[k] = true;
powerSet(k+1);
}실제 코드는 이렇게 된다.
k는 매개변수로 넘겨주고
배열은 전역변수로 어디에서든 읽을 수 있게한다.
매개변수 k는 전체집합에서 k번째 원소부터 나머지 원소가 집합s이고
나머지 원소들 중 include가 true 인 원소들만 포함시켜 출력하라는 의미이다.
base case는 s가 공집합이라면 p를 출력한다. == 배열 include값이 true인 원소들을 출력한다.
일반적인 경우에는
data[k] 를 포함하지 않는경우와
data[k] 를 포함하는 경우로 나누어서 재귀를 돌린다.
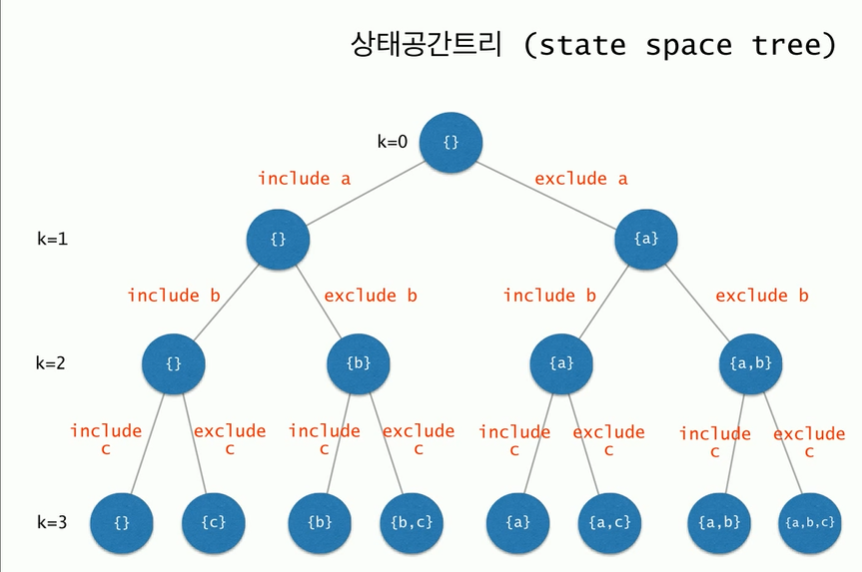
상태공간 트리로 a,b,c의 모든 멱집합을 구하는 과정을 시각화 한 것이다.
a를 포함하는 경우와 안하는경우
b를 포함하는 경우와 안하는 경우 이런식으로 아래로 내려간다.
'알고리즘 with 자바 > 알고리즘' 카테고리의 다른 글
| 문자열 자르기 관련 함수 (0) | 2022.04.25 |
|---|---|
| 순열 (0) | 2021.09.15 |
| Recursion의 응용 : n queen problem (0) | 2021.09.09 |
| Recursion의 응용 : Counting Cells in a Bob (0) | 2021.09.09 |
| Recursion의 개념과 기본 예제들 3 (0) | 2021.09.08 |